Matlab | Algoritma Genetika untuk Komputasi TSP

Berangkat dari artikel sebelumnya, sekarang mari kita belajar bagaimana mengimplementasikan GA pada permasalahan diskrit. menggunakanbil contoh kasus Travelling Salesman Problem (TSP). Kasus TSP merupakan representasi dari masalah graf siklik tertutup dimana titik awal dan titik akhir adalah sama, dengan syarat semua node dilalui masing-masing satu kali. Oleh karena itu, Dibutuhkan rute terpendek untuk menghemat biaya BBM yang sekarang sudah naik Rp 2000/liter *halahhh*. 

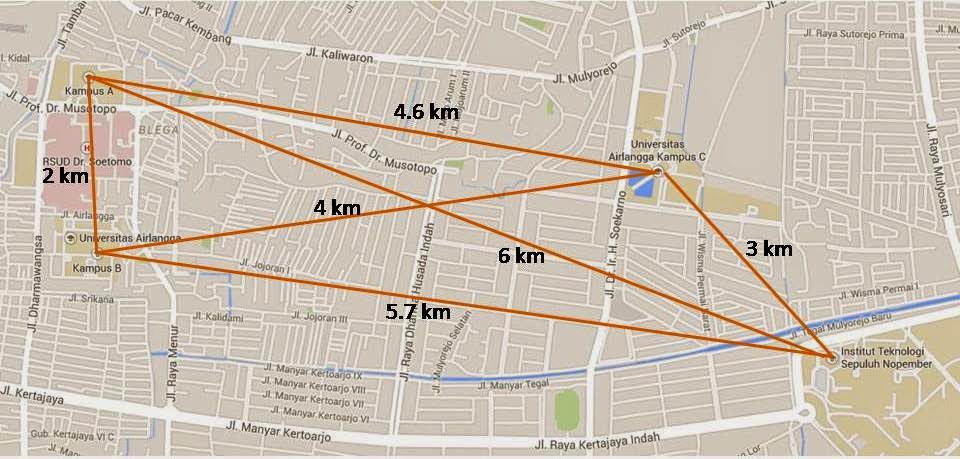
Oke, kita mulai dengan mengambil kasus sederhana. Di sini saya mengambil contoh, bagaimana menghubungkan kampus-kampus saya, yaitu Unair Kampus A, B, C, dan ITS Kampus Sukolilo, Saya capture gambar ini dari maps google untuk mendapatkan kira-kira jarak masing-masing kampus. Dari saya hitung-hitungan dengan mbah maps google, hasilnya adalah sebagai berikut:

Selanjutnya, mari kita asumsikan kampus ini sebagai node. Semisal sebagai berikut:

* Unair A : node 1

* Unair B : node 2

* Unair C : node 3

* ITS : node 4

Sehingga, satu solusi di GA adalah untaian angka permutasi 1 s.d. 4, misal 1 - 3 - 2 - 4. Selanjutnya, mari kita cari rute terpendek antara 4 node tersebut menggunakan GA. Di sini saya menggunakan tools Matlab sebagai contoh komputasi.

Langkah 1: Generate Populasi

Kita set pop_size untuk nilai yang kecil saja yakni 10. Dengan demikian kita mempunyai 10 kromosom dalam populasi.
Contoh:

Langkah 2: Evaluasi Populasi

Evaluasi populasi untuk masalah TSP adalah total jarak yang ditempuh si sales. Jarak tempuh ini kita sebut fungsi tujuan atau objective function. Selanjutnya, dibutuhkan nilai fitness untuk merepresentasikan probabilitas kromosom. Nilai fitness semakin tinggi jika dan hanya jika total jarak semakin kecil. O.k.i perlu dilakukan transformasi pada fungsi tujuan menjadi fungsi fitness. 

Contoh:

Langkah 3: Seleksi

Tahap ini bertujuan untuk mencari kromosom yang akan bercrossover dan bermutasi. Disini akan saya contohkan proses seleksi menggunakan metode 'Turnamen' dengan nilai_tur = 3.

Contoh:

Langkah 4: Crossover

Di sini akan saya contohkan proses crossover dengan satu titik. Sebelumnya, kita pasang nilai random 0 s.d 1 untuk tiap kromosom. Selanjutnya pilih kromosom yang kurang dari Pc. Nah, kita set nilai Pc = 0.8.

Contoh:

Langkah 5: Mutasi

Operator selanjutnya kita lakukan mutasi inversi. Sama halnya dengan crossover, kita pasang nilai random untuk masing-masing kromosom. Kali ini kita set nilai Pm = 0.1.

Contoh:

Langkah 6: Populasi Baru

Tahap terakhir setiap satu iterasi pemilihan kromosom-kromosom terbaik untuk membentuk populasi baru.